Decibelios, mentiras y muestras de sonido
Decibelios, mentiras y muestras de sonido
La producción musical es un arte, y como tal, cierra los ojos y deja que tus dedos suban ese potenciómetro hasta el lugar donde se produce la magia.
Para todo lo demás, sigue leyendo.
Decibelio
Medida logarítmica respecto a un valor de referencia. Es importante decir que es un valor adimensional, es decir, sin unidades.
dB = 10 * log10 ( P1 / P0 )
dB = 20 * log10 ( P1 / P0 )
P1 es el valor de la señal y P0 el valor de referencia
dB SPL
Decibelios de presión sonora. Se toma como presión de referencia (0 dB) 20 μPa en el aiere que corresponde con el umbral de audición del oído humano.
Una onda de 20 μPa son 0 dB:
0dB = 20 * log10 ( 20 μPa / 20 μPa )
140 dB (umbral del dolor) corresponden a:
P = 10^(dB/20) * P0 = 1.97 atmósferas
2 atmósferas sería lo equivalente a estar a una profundidad de 20 metros.
dB FS
dB Full scale. Como valor de referencia se usa el valor máximo de la escala.
Los dB FS son los que se usan en los vúmetros del DAW.
Calcular dB en una onda de 16 bits
Para 16 bits el valor máximo son 2^16 (el valor de la onda puede tomar un valor puntual entre -32767 a 32767). Si el valor máximo de una onda en su pico es 14731, entonces el volumen sería respecto a un valor máximo de escala de 16bits de 32767:
dB = 20 * log10(14731 / 32767) = -7.13
Cómo calcular los decibelios de un audio
dB RMS (dB root mean square)
En lugar de usar un valor puntual (como el de pico), se calcula un valor promedio como la raíz cuadrada de la media de la suma de los cuadrados de las medidas.
dB RMS = √( ⅀dBi² / n)
LUFS
Mide la intensidad de la señal (como los db RMS) pero también tiene en cuenta la sonoridad percibida.
Para tener en cuenta la sonoridad percibida, el cálculo tiene en cuenta las curvas de Fletcher Munson.
Curvas de Fletcher-Munson
Son denominadas curvas isotónicas, representa cómo de sensible es el oído humano a una señal acústica en las diferentes frecuencias.
En ellas se se observa que el oído humano es menos sensible a los graves y los agudos y más a las frecuencias medias.
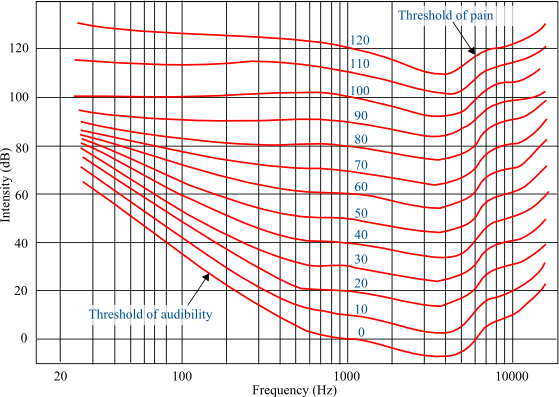
En estas curvas se aprecia que a medida que se aumenta el volumen, las curvas se vuelven más planas.
Tipos de LUFS
Según la duración del muestreo para realizar el cálculo (de mayor a menor duración):
- LUFS-M (LUFS Momentary) - Durante un momento
- LUFS-S (LUFS Short term) - Un momento corto (hay diferencias entre estrofa y estribillo)
- LUFS-I (Integrated) - Valor medio a lo largo de la canción
Niveles LUFS según diferentes plataformas
- Spotify: -14 LUFS
- Apple Music: -16 LUFS
- Amazon Music: -9 a -13 LUFS
- Youtube: -13 a -15 LUFS
- Deezer: -14 a -16 LUFS
- CD: -9 LUFS
- Soundcloud: -8 a -13 LUFS
Señal coherente e incoherente
Coherente si tienen la misma fase
Incoherente distinta fase
Matemáticas con señales y ondas
http://www.sengpielaudio.com/calculator-leveladding.htm
Suma dos señales incoherentes
La y Lb = 10 * log10 ( A/Po + B/Po )
Suma de dos señales coherentes
Dos señales coherentes serían, por ejemplo, las producidas por dos altavoces pegados el uno al lado del otro emitiendo la misma señal:
La y Lb = 20 * log10 ( A/Po + B/Po )
Caso particular dos ondas con el mismo volumen (dB1 = dB2)
dB1 y dB2 = 10 * log10( A/Po + B/Po )
= 10 * log10( 2 * A/Po )
= 10 * log10(2) + log10( A/Po )
dB1 y dB2 = 10 * log10(2) + dB1 = 3.01 + dB1
Conclusión: la suma es unos 3dB más. Es decir, al sumar dos ondas normalmente obtendremos unos 3dB más.
Reducir el volumen de una onda ΔdB
dB = 20 * log10( P/Po ) [1]
dB - ΔdB = 20 * log10( a * P/Po ) [2]
Despejando P/Po en [1] y sustituyendo en [2]
a = 10^(-Δd/20)
Por ejemplo, para bajar -20dB una onda, habrá que multiplicar la señal por 0.1
Headroom y bits de muestreo
Es el espacio que tienes entre el nivel máximo de ganancia y 0dB
16 bits y 24 bits
Con 16 bits tenemos una resolución posible de 2^16 / 2 = 32.768 (valores negativos, positivos y cero de la seña)
Con 24 bits tenemos una resolución posible de 2^24 / 2 = 8.388.608
Como hemos dicho antes, si bajamos el volumen 20 dB, estamos dividiendo las muestras por 10. Así que los valores máximos para 16 y 24 bits serían los siguientes:
16 bits --> 3277
24 bits --> 838.861 (mayor resolución que 16 bits a todo volumen)
Grabación de muestras de instrumentos a 16 bits
Supongamos que dejamos 6dB de headroom en una muestra grabada a 16 bits
dB = 20 * log10(valor_max/32.768) = -6 dB --> valor_max = 16.423
Así que estamos reduciendo nuestra resolución en un 50% con 16.423 valores posibles de 32.768 que teníamos inicialmente.
Grabación de muestra de intrumentos a 24 bits
Si dejamos 6dB de headroom en una muestra grabada a 24 bits
dB = 20 * log10(valor_max/8.388.608) = -6 dB --> valor_max = 4.204.263
Así que estamos reduciendo nuestra resolución en un 50% de 8.388.608 que teniamos en un principio a 4.204.264. Aún así tenemos mucha más resolución que si usasemos toda la escala de 16 bits.
Reaper
El problema de trabajar con una muestra de 16 bits y reducirle el volumen a -20dB es que reducimos el número de posibles valores de 32.768 a 3.277. Eso resulta una disminución de resolución muy elevada. Este problema no existe con muestras a 24 bits.
Afortunádamente DAWs, como Reaper, usan internamente 64 bits. Así que no tendríamos problemas con muestras de 16 bits con buena ganancia, a las cuales reducimos el volumen a -20dB
Como dice stupeT un [hilo sobre trabajar a 16 o 24 bits](https://forum.cockos.com/stupeT en este hilo showthread.php?t=69048):
24 bit recording makes life easy. You dont have to fine tune and gain stage the signals to perfection when you record as you had to do with 16 bit.
The fact that REAPER internally works with 64 bit leads to the least possible summing/rounding errors while mixing. Another great benefit: Did you notice, that REAPER does not distort when you level a track to say +10 dB? Yeah, internal channels/tracks have plenty of headroom! Thats great and very much like in analog consoles. Again: makes life easy.
In a simple setup the master channel will be the only one where you have to stay below 0dB, because this one will drive the DA-converters which will have to use 24 bit (or 16). Dont forget to dither here as the very last plugin in the master FX chain.
Volúmenes relativos en la mezcla
Volumen de la voz humana a 1ft (0,3m) de distancia:
- Normal: 70 dB
- Elevada: 76 dB
- Muy fuerte: 82 dB
- Chillando: 88 dB
Como se puede ver en los datos anteriores, se toma como elevar la voz, subir 6dB.
Por otro lada, ¿cuál es la mínima diferencia de dB que un ser humano puede detectar? Haciendo el test mínima diferencia de volumen que un ser humano puede detectar podemos decir que 1dB de diferencia empieza a no ser apreciable.
Así que cuando estemos hablando de subir el volumen, al menos tendrá que ser 1dB.
Sensibilidad de un altavoz
Esta parte ya está fuera de nuestro DAW.
Sirve para saber cuántos decibelios SPL dará un altavoz en su eje a un 1m de distancia al inyecrtarle una señal de audio eléctrica de 1W.
Se expresa en dB/1W/1m.
Suele rondar los 90 dB.
Sensibilidad del Altavoz
Conclusiones
Usar 24 bits.
La suma de dos ondas que tienen el mismo valor de dBs será 3 dB más que los dBs de una de ellas.
10 ondas con los mismos dB aumentan la salida en 10 dB
30 ondas con los mismos dB aumentan la salida en 14.7 dB
Calculadora suma de 10 ondas incoherentes
Calculadora suma de 30 ondas incoherentes
Regla de los volúmenes
En el DAW, todo en dB(FS) y lo que mide el vúmetro correspondiente (no el nivel que hayamos puesto en el fader)
Volumen máximo grabación instrumento < -6 dB
Volumen máximo cada pista < -20 dB
Volumen máximo mezcla < -6 dB
Volumen máximo mezcla masterizada = 0 dB
Con el volumen de pistas a -20 dB, nos aseguramos que aunque tuviésemos 30 muestras, una en cada pista, como mucho, llegaremos a -5,3 dB en el máster.
Referencias
Headroom
https://blog.landr.com/es/7-trucos-para-crear-headroom/
https://es.wikipedia.org/wiki/Decibelio
Calibrar monitores según Bob Katz
Monitor Calibration with K-System
dB RMS
https://www.hispasonic.com/foros/niveles-ganancia-grabacion-exportacion/419071
https://www.youtube.com/watch?v=_s2vkOOMwo0
https://www.youtube.com/watch?v=Pmn_ZJ1pdfg